Publications and Preprints
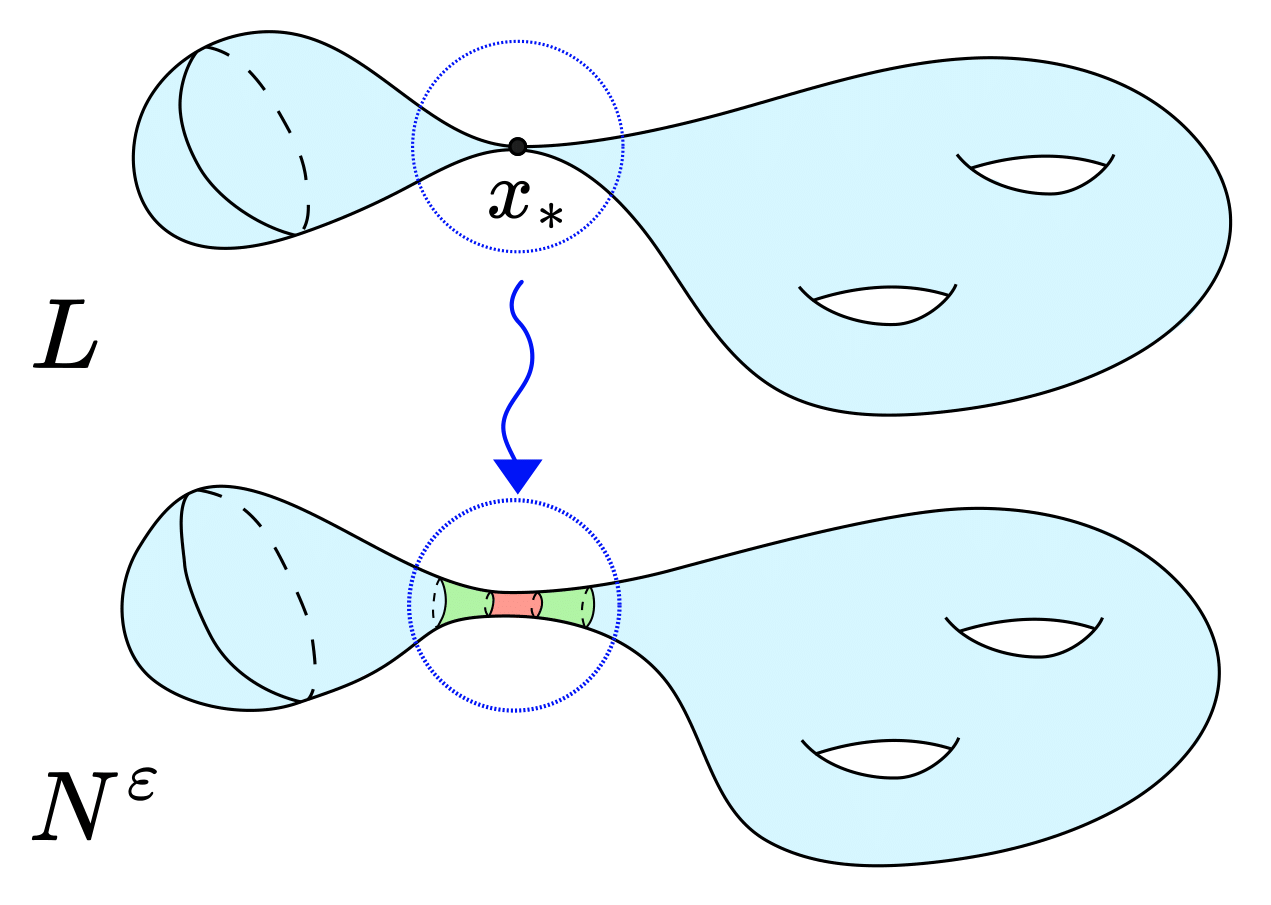
4. Infinite-Time Singularities of the Lagrangian Mean Curvature Flow
Wei-Bo Su, Chung-Jun Tsai, Albert Wood
Abstract: We exhibit examples of Lagrangian mean curvature flow which exist and are embedded for all time, but form an infinite-time singularity and converge to an immersed special Lagrangian as \(t\rightarrow \infty\) This result shows that infinite-time singularities can form in the Thomas--Yau `semi-stable' situation. Our work is a parabolic analogue of the results of Dominic Joyce and Yng-Ing Lee regarding desingularisation of special Lagrangians with conical singularities. The gluing construction that we employ is inspired by the work of Simon Brendle and Nikolaos Kapouleas regarding ancient solutions of the Ricci flow.
3. Cohomogeneity-One Lagrangian Mean Curvature Flow
Jesse Madnick, Albert Wood
Video Lectures: S02T02 Albert Wood
Abstract: We study mean curvature flow of Lagrangians in \(\mathbb{C}^n\) that are cohomogeneity-one under a compact Lie group \(G\leq SU(n)\) acting linearly on \(\mathbb{C}^n\). Each such Lagrangian necessarily lies in a level set \(\mu^{-1}(\xi)\) of the standard moment map \(\mu:\mathbb{C}^n\rightarrow \mathfrak{g}^*\), and mean curvature flow preserves this containment. We classify all cohomogeneity-one self-similarly shrinking, expanding and translating solutions to the flow, as well as cohomogeneity-one smooth special Lagrangians lying in \(\mu^{-1}(0)\). Restricting to the case of almost-calibrated flows in the zero level set \(\mu^{-1}(0)\), we classify finite-time singularities, explicitly describing the Type I and Type II blowup models. Finally, given any cohomogeneity-one special Lagrangian submanifold in \(\mu^{-1}(0)\), we show it occurs as the Type II blowup model of a Lagrangian MCF singularity, thereby providing infinitely many previously unobserved singularity models. Throughout, we give explicit examples of suitable group actions, including a complete list in the case of \(G\) simple.
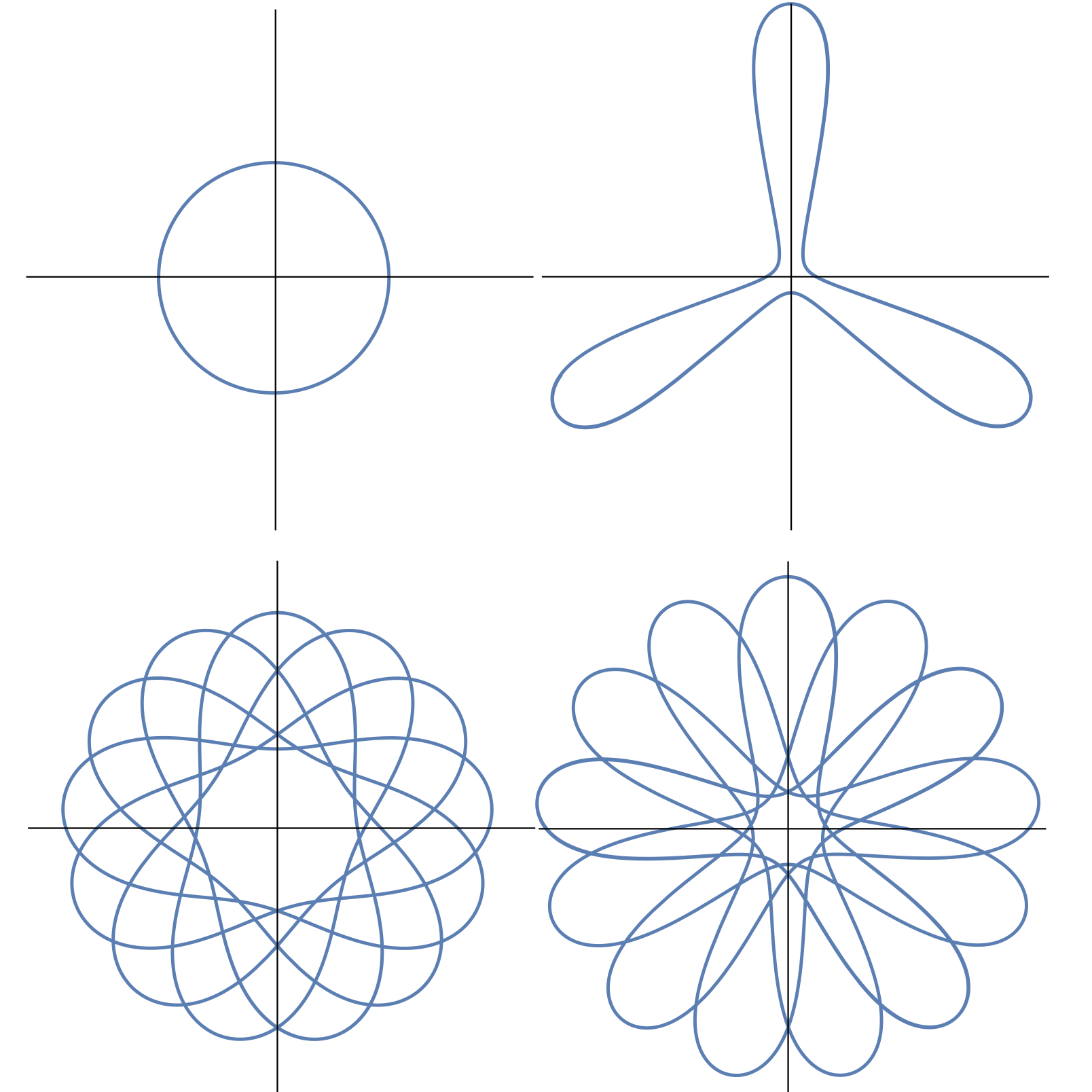
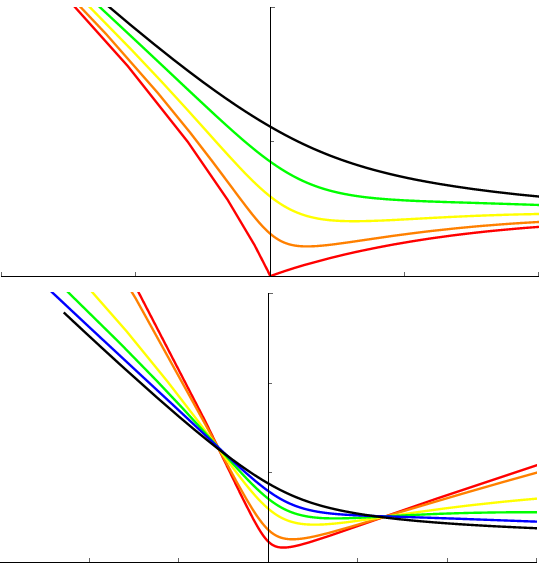
2. Singularities of Equivariant Lagrangian Mean Curvature Flow
Comm. Anal. Geom. (to appear), Albert Wood
Video Lectures: [1st GAF] Albert Wood: Singularities of Lagrangian Mean Curvature Flow
Abstract: We study almost-calibrated, \(O(n)\)-equivariant Lagrangian mean curvature flow in \(\mathbb{C}^n\), and prove structural theorems about the Type I and Type II blowups of finite-time singularities. In particular, we prove that any Type I blowup of such a flow must be a special Lagrangian pair of transversely intersecting planes, any Type II blowup must be the Lawlor neck with the same asymptotes, and these blowups are independent of the choice of rescaling. We also give a partial classification of when singularities occur in the equivariant case, and examine the intermediate scales between the Type I and Type II models.
1. Lagrangian Mean Curvature Flow with Boundary
Calc. Var. 61, 106 (2022), Chris Evans, Ben Lambert, Albert Wood
Video Lectures: [3rd GAF MC] Albert Wood: Lagrangian Mean Curvature Flow with Boundary
Abstract: We introduce Lagrangian mean curvature flow with boundary in Calabi-Yau manifolds by defining a natural mixed Dirichlet-Neumann boundary condition, and prove that under this flow, the Lagrangian condition is preserved. We also study in detail the flow of equivariant Lagrangian discs with boundary on the Lawlor neck and the self-shrinking Clifford torus, and demonstrate long-time existence and convergence of the flow in the first instance and of the rescaled flow in the second.
PhD Thesis
Singularities of Lagrangian Mean Curvature Flow
PhD Thesis, completed as part of the PhD Degree at University College London
Supervised by Prof. Felix Schulze
I was awarded my PhD in September 2022 from University College London. The topic of my thesis is Lagrangian mean curvature flow, focusing on singular behaviour and boundary conditions for the flow. When writing my thesis, I aimed to create a resource suitable for newcomers learning the subject of Lagrangian mean curvature flow for the first time; in particular I provided motivating material from the theory of mean curvature flow as well as an exposition of the original proof by Smoczyk of the preservation of the Lagrangian condition. If you would like to read it or view the abstract, please click on the title above.
Short Research Projects
3. On Belyi Functions and their Applications
Short Project, completed as part of the LSGNT Doctoral School
Supervised by Prof. Andrew Granville, Dr. Davoud Cheraghi
Abstract: We examine the application of the theory of dessins d'enfant to the problem of bounding the difference of coprime polynomials. The existence of a sharp bound is equated to the existence of a particular multigraph, which is tractable with basic combinatorial techniques.
2. Collapse in Riemannian Geometry
Short Project, completed as part of the LSGNT Doctoral School, with Fabian Lehmann, Jenny Swinson
Supervised by Prof. Mark Haskins, Prof. Jason Lotay
Abstract: We give an exposition on the phenomenon of collapsing Riemannian metrics with bounded sectional curvature, focusing on the important contributions of Cheeger-Gromov and Foscolo.
1. Combinatorial Applications of Szemerédi's Regularity Lemma
Master's Thesis, completed as part of the MMath Degree at University of Oxford
Supervised by Prof. Ben Green
Abstract: Szemerédi’s Regularity Lemma is a result of extremal graph theory, which roughly states that all graphs can be partitioned such that the edges between the partition sets appear to have been generated at random. It therefore helps us when the result we are trying to prove is expected to be true for random graphs. In this dissertation, we cover some applications of Szemerédi’s Regularity Lemma to number theory and additive combinatorics.
Examples of Cohomogeneity-One Shrinkers for LMCF in \(\mathbb{C}^n\)
In our work, we consider an action of a Lie group \(G \circlearrowright \mathbb{C}^n\), and Lagrangians which are cohomogeneity-one with respect to this action - i.e. one-parameter families of orbits. A concrete example is given by \(O(n)\)-equivariant Lagrangians in \(\mathbb{C}^n\), which are necessarily cohomogeneity-one. This special case is well-studied, for example the \(O(n)\)-equivariant shrinking solitons for Lagrangian mean curvature flow were classified by Anciaux, Castro and Romon, and the image depicts the 'profile curves' of a selection of their shrinkers, i.e. the intersection of the shrinkers with the plane \(\mathbb{C}\times \{0\}^{n-1}\).
We show that in general, cohomogeneity-one Lagrangian shrinkers are characterised with their intersection with a carefully chosen complex line \(P \subset \mathbb{C}^n\), which we call the 'profile curve' of the Lagrangian. The profile curve of a cohomogeneity-one shrinker must satisfy an elliptic PDE, which remarkably does not depend on the group \(G\). Therefore, the classification by Anciaux, Castro and Romon is in fact a classification of all cohomogeneity-one shrinkers. By considering these curves as subsets of \(\mathbb{C}^n\), one recovers the Lagrangian shrinkers by applying the \(G\) action.
A Type II Blowup of an LMCF Singularity
Lagrangian mean curvature flow typically forms finite-time singularities, meaning that at a finite time, the curvature of the Lagrangian submanifold becomes unbounded and the flow cannot be continued smoothly. To analyse the geometric structure of these singularities, one may perform a 'Type II blowup', by considering a sequence of rescalings which converge to a limiting eternal smooth flow.
In the case of almost-calibrated \(O(n)\)-equivariant Lagrangian mean curvature flow in \(\mathbb{C}^n\), my work shows that a singularity must occur at the origin, and there is only one possible singularity type - the Type II blowup must be the \(O(n)\)-equivariant Lawlor Neck.
The image depicts an example of such a singularity forming. In the upper image, the flow (with initial condition in black) forms a finite-time singularity at the origin. The lower image depicts the Type II rescalings of this flow at a fixed time, which can be seen to approach the Lawlor neck.
\(O(n)\)-Equivariant Examples of LMCF with Boundary
This image shows the behaviour of Lagrangian mean curvature flow with boundary in \(\mathbb{C}^n\), in the special case of \(O(n)\)-equivariant Lagrangians. The curves shown in the picture are 'profile curves', given by the intersection of the \(O(n)\)-equivariant Lagrangians with the plane \(\mathbb{C}\times \{0\}^{n-1}\). The red curves represent the initial condition.
In the upper images, the boundary condition is the \(O(n)\)-equivariant Lawlor neck. It can be shown that the flow exists for all time and converges to a static special Lagrangian disc.
In the lower images, the boundary condition is the \(O(n)\)-equivariant Clifford torus, which shrinks under the flow - the depicted flow of curves is a rescaled flow. In this case, the numerical evidence suggests long-time existence and convergence of the rescaled flow to a rotating soliton. The speed of the resulting soliton corresponds to the angle of the boundary condition, as can be seen from the images.
